Drake's

前面講到M如果會變成無限大，就無法滿足能夠學習的理論，所以我們希望能透過成長函式mH(N)來取代M，這一講主要在推論mH(N)是不是真的成長的比較慢，且能夠夠取代掉M

複習一下成長函數的定義是指Hyperthesis集合在N個點上最多能夠產生多少個Dichotomies(即O或是X兩分的排列組合)。上一講提到了四種成長函數，且每一種都可能有出現break point現象，就是指當輸入點數大於某個臨界值後，會產生沒有辦法滿足的Dicotomies組合。

假設今天有一個Hyperthesis在N為1時mH(N)為2種，N為2時mH(N)最多只有3種(3 < 2^2)，那麼我們要找在3點輸入時，而且最小的break point K為2(即任2點不能有shatter)，究竟mH(N)為多少呢？可以發現加上第5種組合，無論前面4種用什麼組合，在第5種任2點都會shatter，所以最多只會有4種可能

到這邊可以發現當N越大時，break point K會對最大可能的mH(N)產生限制(因為K為break point，K+1開始都會shatter)，使得當N越大時，N和mH(N)之間的差距會越來越大。所以如果可以證明mH(N)是一個多項式，就可以在原本的Hoeffiding不等式中，把可能無限大的M取代成有限制且為多項式的mH(N)，使得學習是有可能的。

再來先別管成長函式了，我們透過bounding function來表示在break point為K的情況下，mH(N)的最大可能性，就是在K個點不能出現shatter。這樣我們就可以不用管問題是屬於positive intervals或是1D perceptrons要用不同的方法分析，我們可以統一使用B(N, 3)來表代所有不同的問題。

N和K建立的bounding function可以用表格來呈現，基本上可以分成4種。第一種是如果K為1，即B(N, 1)代表1個點不能出現shatter，那麼只會有1種情況；第二種是右上斜角部份，今天如果K大於N，那麼K等於沒有限制，所以最多會有2^N種情況；第三種是在斜角上，當N和k的值一樣時，因為不能是2^N種，所以減1最多會有2^N-1種。

那麼最重要的斜角下方部份該怎麼填了，假設要填的值是B(4, 3)，我們猜測他可能和前一排的B(3, ?)有關係。這裡可以看到所有的組合總共是11種，看起來B(4, 3)好像是B(3, 3)和B(3, 2)相加，但是該怎麼去證明說是有關係的呢？

把B(4, 3)的11種解可以分成α和β兩種類型，橘色的類型為X1-X3相同，但是X4會不一樣(即2α)，紫色的類型為皆不相同(即β)。B(4, 3)指其中3個點不能shatter，那X1-X3也是其中的3個點，所以也不能shatter，意思就是說如果今天不看X4的話，因為X1-X3不能shatter，所以α加β會小於等於B(3, 3)。

再繼續往下只看α部份的話，如果X1-X3其中有2個點shatter了，那麼再加上X4的話就會造成3點shatter，這也是B(4, 3)不允許的，所以X1-X3其中2個點也不能shatter。於是α會小於等於B(3, 2)

再來就可以把中間證明的過程連結在一起了，B(4, 3) ≤ B(3, 3) + B(3, 2)，又可以轉變成B(N, K) ≤ B(N-1, K) + B(N-1, K-1)，這樣就可以把斜角下方都值都可以填上一個上限值。我們最早從會有無限多組解的大M開始，再到其實大M是有限的，透過成長函數可找到dichotomy數量mH(N)，再推展到上限函式B(K, N)來統一計算N和K的上限值(不用依不同的情況計算mH(N))，最後證明到這裡的值其實就是上限的上限值(很繞口)。

所以推展到這邊可以得到的重點是，mH(N)會被上限函式bounded住，然後這個上限函式又會被上限的上限bounded住，而且這個上限的上限是一個多項式；因此只要確保有出現break point，就可以說mH(N)是個多項式。

再來回到原本的帶有union bound的Hoeffding不等式，我們經過上面的推導後，是不是可以把這個成長函式mH(N)丟進Hoeffding裡面，就可以了呢？再來會開始推導成投影片中的新的式子，是一個長的差不多的式子，他可以證明在N夠大的情況下，就可以根據Hoeffding不等式來說學習是可以達成的。

第一步遇到的問題是Eout會是無限多的值，所以會先把Eout取代成有限的Ein’，這裡的概念是如果Ein和Eout差距很大時(即壞事發生時)，那麼有很大的機會(>1/2)，Ein和Ein’也隔的很遠。

接著第一步的結果，因為多了Ein’所以會多了N個樣本，所以成長函式裡面的N會變成2N。第二步會把Union Bounded中發生各種壞事的情況，找到共同發生的部份，所以把前面說到有限組合的mH(N)代進式子中。

再來因為我們是有限多個值了，所以想像概念就像是現在瓶子裡面有2N個樣本，今天抽出N個樣本，我們就可以把這N個樣本和原本的2N個樣本作比較。這就像是用了一個比較小的瓶子和比較小的誤差，使用了抽後不放回的Hoeffding，他其實還是Hoeffding。

證明到這邊，可以簡單的證明出apnik-Chervonenkis (VC) bound了! 所以在break point為4的2D perceptrons中，如果N夠大的情況下，是真的可以透過PLA達到學習效果的。

總結來說，這一課證明了只要存在break point，就會對未來的成長函數加上很大的限制，因為有了break poin也才能證明mH(N)會被一個多項式的上限函式bounded住，並且mH(N)可以取代Hoeffding原本是無限多的大M

參考資料:
Machine Learning Foundation 06

這一講主要在延續前一講的推導，說明無限多個hypothesis到底發生什麼事情。

前面有是到如果要讓訓練是可行的，則必需要加上一些假設，首先原本訓練的資料和測試hypothesis的資料都是來自於相同的分配(Distribution)，那麼當hypothesis集合是有限的，且資料數量N夠大的情況下，不論演算法A挑出哪一個函式g，Ein和Eout都會是接近的。在這個情況下，只要挑出趨近於0的Ein，就可以保證Eout也趨近於0，即代表學習是可能的。

再複習一下到目前的學習內容。證明機器學習的過程中，首先會希望得到一個函式g而且和f會很接近，也就是希望Eout(g)會接近於0。但是我們不知道該怎麼去證明Eout會接近於0，於是我們從取樣下手來證明Ein如果趨近於0的話，且Ein和Eout會很接近，那麼Eout也會趨近於0。那麼要讓機器學習可能，其中一個很大的重點是有限的hypothesis集合M，究竟這個M扮演了什麼角色？

這時我們會談到M的trade-off，所謂選擇M的trade-off就是當我們選了比較小的M才能符合Hoeffiding不等式讓壞事發生的機率降低，但這代表可以選擇的hypothesis比較少，也許這樣可能就無法選到一個好的hypothesis來讓Ein可以趨近於0。相反的，如果M越大，雖然選擇的hypothesis變多，但是壞事發生的機率也會上升。所以選擇一個正確而且適當的M對於學習問題是很重要的。

前面提到如果M是有限的集合，那麼學習才有可能發生，如果是M是無限大的話，壞事發生的機率也就是無限大，機器就沒辦法學到一個好的結果，因為其中的壞事發生的機率，就是M種發生壞事的機率相加。雖然看起來M會無限大，但事實上發生不同壞事資料D可能是一樣的。以PLA為例說明，假設選了兩條非常接近的線(即兩個hypothesis)，其實這兩條線可能對於同一組資料D分出來的結果是一樣的，所以不同的壞事發生可能會有重疊的情況，所以看起來M應該是有限的。

假設平面上只有一個點，每條線都是一個hypothesis，看起來你確實可以在平面上切出無限多條線，可是事實上不管怎麼切都只會有兩種情況，即這個點不是O就是X，所以只要任何長的像H1的切線都是O，任何長的像H2的切線都是X

如果是兩個輸入的話，總共會有4種切線，

如果是3個輸入呢？看起來總共會有8種總合，但是事實上其中會有2種組合沒辦法使用直線切出來(OXO和XOX)，所以實際上只會有6種切線。

這又稱為Effect Number of Lines，從表格可以發現每個輸入最多只會有2^N種組合，但是能夠有效的切出兩種分類會從3個輸入開始變少，所以我們可以把M取代成effect(N)。也就是說無論今天的M再多大，都可以找到一個有限的切線數量effect(N)，而且這個effect(N)可以比2^N小很多，這樣就能夠保證學習能夠發生。

這裡講到Dichotomy的概念，所謂Dichotomy就是兩分的意思(分成O和X為一例)，Dichotomy和原本的hypothesis的差別在於Dichotomy是有限的組合，而Hypothesis是平面上無限條線的任一條，接下來會把原本的M取代成有限的Dichotomy數量。

接著會透過計算成長函式(Growth Function)來找到有限的Dichotomy上限數量，取代M讓學習可以發生。

以一個最簡單的Postive Ray來說明，資料點N分佈在一維線上，當我們取一個threshold可以找到不同的Postive Ray，那麼所有可能的Dichotomy組合總共會是N+1個(就是能在點之間切線的數量)，在這個問題下Dichotomy的組合大大的小於2^N種。

課程舉了四種不同的成長函數，其中PLA的Dichotomy數量mH(N)會小於2^N，但是對於Hoeffding不等式中，如果mH(N)是指數型成長，則無法確保不等式成立，所以我們需要證明mH(N)是一個多項式的成長。

這個部份提到了Break Point的概念，所謂的Break Point就是當某一個輸入開始，Dichotomy數量不再是指數成長(即2^N)，像是positive ray在2個輸入時發生，postive interval在3個輸入時發生，2D perceptrons在4個輸入時發生。在這裡看到神奇的地方在於本來的沒有break point的情況下mH(N)會是指數成長，但是當有了break point後，mH(N)會是一個多項式，下一講就會開始證明是如何轉變成多項式的。

參考資料:
Machine Learning Foundation 05

這一講的學習重點主要是在如何討論學習到底是不是可行的，並進一步推導證明機器是真的可以「學習」的。

機器會不會其實是沒辦法學習的？我們可以先看講義上的圖形，上半部的圖形屬於-1，下半部的圖形屬於+1，那麼給了f上方右邊的圖，他究竟是屬於+1還是-1呢？如果我們用黑色區域是不是對稱來判斷，那麼這張圖會是+1；但如果我們用左上角的格子是否為黑色，那邊這張圖會是-1。這裡會發現如果我們用不同的規則就可能得到不同的答案，看起來好像真的沒辦法讓機器真的「學習」一個正確的答案。

用一個比較數學的例子來看，假設今天有一個函式f，輸入是3個bit，輸出是o或是x。再來我們透過機器學習演算法學到g函式，並確保這個g函式在5筆資料D都能和f得到一樣的答案(即f和g結果相同)。所以我們確保了g和f(甚至是講義上的8個f)在D得到相同答案，但是除了D之外剩下的3種答案，g只會有一種結果。這會有什麼的影響呢？比如說當g在剩下3筆得到XOX，那麼他會和f6相同，可是我們今天是要告訴你正確的f其實是除了f6以外的函式，那麼似乎g和f答案又錯了，看起來機器好像真的沒辦法「學習」到一個正確答案。這又稱為no free lunch，如果沒有對機器學習問題加上一些限制，即我們只是單純給機器資料學習，事實上是沒辦法讓機器學出一個正確的答案的。

這裡舉一個推論未知的方法，比如說在一個瓶子中有綠色彈珠和橘色彈珠，如果今天沒有辦法完全數完瓶內所有的彈珠，那麼該如何去推論橘色彈珠的比例呢？我們可以透過統計手法利用取樣(樣本)的比例來推論瓶內橘色彈珠(母體)的比例。假設瓶內橘色彈珠的比例是μ，綠色是1-μ，取樣出橘色彈珠的比例是ν，綠色是1-ν，是否可以用這個ν來推論μ呢？照理說ν可能沒辦法完全的推論μ(明明有橘色彈珠，但是每一次運氣不好都抽到綠色)，但是在一定的機率下，ν應該是有辦法推論μ的，在數學上可用Hoeffding’s Inequality來解釋

透過Hoeffding’s Inequality可以解釋，如果今天抽出彈珠(N)的數量越大的話，ν和μ之間差很遠的機率(ε)就會很小，也就是說如果可以取出數量夠大的樣本的話，就可以讓「壞事」(ν和μ差很多)發生的機率變小，我們可以說ν和μ大概差不多會是對的(即probably approximately correct, PAC)

那用這個抽彈珠的例子到底和學習會有什麼關係？當把抽彈珠轉成學習的問題，未知橘色彈珠的機率μ可視為未知的f，所有抽出來的彈珠就是每筆的資料，其中橘色彈珠可視為h(x)≠f(x)，即hypothesis h是錯的，綠色彈珠可視為h(x)=f(x)，即hypothesis h是對的。所以如果我們在獨立的抽出彈珠時，就可知道來誰論h和f不一樣的機率到底是多少。

所以把前面錯誤推估的部份加入進去機器學習的流程中。首先我有一個機率在瓶子中取樣產生了資料D，在判斷h和f是不是一樣時，其中這個h就是Hypothesis集合中的其中一個

再來就可以透過手上確實知道的資料D來說h和f是否相同，也就是透過Ein(取樣的資料Error)來推論Eout(實際的瓶子的資料Error)，使用Hoeffding’s Inequality就可以證明當N夠大時，Ein和Eout就會差不多是相同的。

但這樣的證明充其量其能說是驗證而已，就是這個h目前還沒有辦法像是PLA一樣丟不同資料產生不同的h，但是我們可以證明這個h是不是使用資料D能夠有有用的推論f，即驗證選出h的表現是好的還是不好的。

目前已經可以驗證相同h之下的表現好還是不好，但是今天當我們有了選擇時(即在多個h裡面作選擇)，我們可能就會有偏見的選出一個瓶子都是綠色彈珠的結果，但事實上可能只是剛好這個瓶子都「碰巧」的抽出了綠色彈珠，就像擲銅板一樣，不論這枚銅板多麼公正，都會有可能出現每次都正面的情況。前面講到Hoeffding告訴我們的是ν和μ之間差異很大的這種「不好」的事情機率應該是很小的，但是當我們有選擇的時候，這種「不好」的取樣卻會造成Ein和Eout差距變大。

如果演算法遇到不好的資料(Ein和Eout差很遠)，就會得到不好的結果。Hoeffding告訴我們的是每一個h不好的情況是很小的，但是在演算法有自由選擇h的情況下，那麼不好資料發生的機率是多少呢？

假設有M總不同的h，那麼不好資料發生的機率，就會等於每一個h發生不好機率的總合(Union Bound)。所以如果演算法有辦法選出一個最小的Ein(壞事發生的機率是最小的)，就可以表示選出來的Eout會是最小的

總結來說機器該如何能夠學習呢？只要滿足Hypothesis集合是有限的集合M，且樣本資料N是夠大的，對於任何被演算法選出來的g(其中一個假設h)，就可以推論Eout和Ein是差不多相同的。就是剛提到的，演算法只要選出一個Ein是最小的，就可以保證Eout也是最小的。

參考資料:
Machine Learning Foundation 04

第三講主要在說明機器學習有哪些種類，以及在訓練過程中會用到哪些不同的特徵(Feature)種類。在針對輸出空間y的不同可以有以下幾種不同的學習種類：

在上一講有看到在平面上透過直線切割出兩種類別，這種二元分類(Binary Classification)是機器學習裡面最常見的問題。但現實上的應用有時並不會侷限在二元分類，常常會遇到多種類別的問題，即多元分類(Multiclass Classification)問題。比如說，可以透過硬幣的大小和重量來區分出美元硬幣，這時候的輸出就是4種類別，如果把類別數量用K來代稱，那麼二元分類可以被視為多元分類的一種特例。這種多元分類問題常用在許多不同的應用，比如說手寫字跡的辨識、圖片中的物件辨識或是email的種類或是重要性辨識。

如果今天要預測的不是兩元類別或是多元類別，而是一個數字型態的資料，例如透過公司的資料或是新聞的風向來預測股價，或是透過氣候的資料來預測未來的氣溫，這樣的學習也是在統計中常被使用到的迴歸分析。通常透過迴歸分析來預測數值結果也是一種具有label的監督式(Supervised)的學習，因為在學習過程中，會告訴演算法資料x的特徵，和其對應的y數值結果。

再進一步更複雜的應用中，像是自然語言辨識的領域中，如何對每個字作詞性標注(Part-of-Speech Tag)，他看起似乎像是種多類別的問題(一個詞被分到其中一種詞性)，但是這種詞性標注的問題往往不是把每個詞拆開來輸入，而是會把整個句子輸入來學習分析，因為詞性可能會根據語句而有變化，這個問題尤其是在中文詞性標注更加的明顯。傳統上處理詞性標注可以逶過隱馬可夫模型(Hidden Markov Model, HMM))將詞當作觀察現象，詞性當作隱藏狀態，並結合維特比(Viterbi)演算法來作詞性標注。

在學習的過程中有沒有給予y(輸出標籤)，可以區分成監督式和非監督式學習。

之前討論到的學習方法是，我們把每個硬幣x的大小和重量，以及這個硬幣的種類y，來學習判斷硬幣的哪個種類，這種有給予y的稱為監督式學習。如果今天不告訴機器每個硬幣的種類y，在只知道硬幣的大小和重量的情況下，把硬幣區分成不同群，稱為非監督式學習。非監督式學習困難的問題常常在於分群的結果不容易被衡量，監督式學習效果的衡量可以簡單的比對機器判斷的g(x)和y是否一致，因此非監督式常習會再透過一些方法像是Elbow Method或是silhouette analysis來判斷分群的品質。非監督式學習除了群聚分析外，像是密度分析(Density Estimation)和臨群偵測(Outlier Detection)也都是非監督式學習的範疇。

介於監督式和非監督式學習中間稱為半監督式(Semi-supervised)，半監督式會先使用一部份已經有標注好標籤的資料作監督式學習，再使用沒有標注的資料來讓機器可以學的更好。其中常用在大量的資料無法將所有的資料都給予標籤，因為標注資料的成本是很高的，所以像是影像辯識就會透過半監督式方法來完成學習。

增強學習(Reinforcement Learning)會透過獎勵的方式告訴機器什麼樣的情況是好或是不好，例如在廣告的投放上當使用者點擊某種類的廣告會影響廣告系統推薦給使用者的廣告內容。

參考資料:
Machine Learning Foundation 03

第二講的內容主要在說明如何透過機器學習來回答兩元問題。上一講有提到機器學習會透過一個演算法A，並透過資料D和假說Hyposis H集合，透過選擇一個假說來學習到函式g。以上一講的案例來說，我們會透過函式g來決定要不要發信用卡。

我們可以簡單的透過計算分數的方式來建立一個簡單的機器學習方法。首先可以把每位使用者的資料建立一筆特徵向量當作輸入資料，而每個維度還會有重要性的權重(例如年薪的權重可能會比性別的權重還來的高)，最後把每個使用者依據加總的分數，和設定的門檻值(threshold)比較，如果高過門檻值就發卡，沒高過就不發卡，這樣的模型h就是一個簡單的Perceptron(感知器)。

其實在情感分析(Sentiment Analysis)上，以前也常用這種計算分數的方式來判斷文本屬於正面(Postive)或是(Nagtive)。當我們手上有一個情感詞典(定義哪些字是正面，哪些字是負面)，在拿到一篇文章的時候，就可以加總正面詞(+1)和負面詞(-1)來算出文章的情感分數，再搭配門檻值來判斷文章是屬於正面還是負面，甚至是正負面的程度。(不同字詞可以有不同程度的權重，沒有被情感詞典定義的詞當作0分)

這個用來判斷要不要發信用卡的模型h，在二維的平面上會呈現為一條直線(平面上的每一點就是一筆資料x，每一筆資料的形狀則是指的label)，在高維度的空間會是一個平面。這條直接的一邊是其中一種label(O)，跨過線的另一邊則是另一種label(X)，這樣的線性分類器即可以用來分類兩元問題。

那究竟平面上面的這條線該怎麼切才是最好的呢？可以透過Perceptron Learning Algorithm(PLA)來學習出最好的線性分類器。當平面上的線如果切的不夠好時，透過會旋轉這條線來讓切線更完美。當正的label被分到負的label時，代表w和x的角度太大，可以透過向量相加來讓角度變小；當負的label被分到正的label時，代表w和x的角度太小，可以透過向量相減來讓角度變大。就這樣一直轉到所有的正的label和負的label都分到正確的類別沒有任何分錯，就可以得到一個最佳的切線，這個演算法稱為PLA。

PLA既然要在平面上找到一條切線，那勢必他就必須要是線性可分的問題，像是上圖最左邊就是一個線性可分的問題，右邊兩張則是線性不可分，即不管怎麼旋轉這條切線都沒辦法把兩種類別各自分到對的地方。如果稍有瞭解支援向量機(Support Vector Machine, SVM)的人大概會想到，如果使用SVM的話就可以解決線性不可分的問題，因為SVM主要是也在空間裡找到線性可分的超平面來切分空間，如果遇到第二種線性不可分的情況，最簡單可以透過調整懲罰參數C來忽略一些無法分到正確類別的資料(也許是雜訊)。至於遇到第三種情況的話，則可以調整核函式Kernel Function來將於N維線性不可分的資料於較高的維度M找到線性可分的超平面。

回到PLA，現實上絕對沒有這麼好的情況可以讓你都有線性可分，也許只有稍微有點雜訊，就會讓問題變成線性不可分。這邊會用到演算法稱為口袋演算法(pocket algorithm)，即是在PLA的修正學習過程中，如果找到一個比較好的線(即分錯最少)，我們就把這條線放到口袋裡面，當遇到下一條比我們口袋裡這條線更好的線，就再換成新的線，一直到執到覺得應該差不多就停下來。所以當我們是線性可分，PLA可以幫助找到好的解答；但如果不是線性可分，透過變形的PLA確實可以找到一個還不錯的解答。

參考資料: Machine Learning Foundation 02

林軒田老師的機器學習基石(Machine Learning Foundation)又開始在Coursera上開課囉!雖然老師已經在youtube上公開所有的課程影片還有課程Slide了，不過在Coursera上面跟著每周的課程，也滿有上課的感覺！剛好也針對上課的內容，希望在有時間之餘，隨手寫下一些其中自己覺得印象深刻的部份來加深對機器學習的瞭解。在第一講裡面談到了機器學習的背景，機器學習的過程是從資料出發，經過計算後可以得到某種表現的增進。比如說我們透過股市的資料，經過計算後讓電腦自動投資，來賺到更多的錢。那什麼時候該使用機器學習，其中有提到三個關鍵：

1. 資料或問題有潛藏的模式(Pattern)可以學習，並得到某種表現的增進
2. 具有存在的規則，但我們無法得知該如何(或是簡單的)定義
3. 需要有資料，因為機器學習需要從資料來學習潛在的規則

上面共有四個問題，讓我們思考倒底什麼時候可以使用機器學習(答案是3)。

1. 預測小孩下次什麼時候哭，因為是沒有pattern所以無法使用機器學習
2. 要判斷一個graph裡面是否有cycle，其實寫程式就可以判斷，而不用使用到機器學習
3. 判斷是否要核信用卡，其中包含了pattern，而且不容易被定義，且可以使用歷史資料來學習
4. 核能是否會毀滅地球，這個問題太有爭議性而且也沒有足夠的資料來學習

在看機器學習的流程前，機器學習有幾個重要的定義:
x: 機器學習的輸入資料，會透過這些輸入作學習
y: 我們想要機器學習告訴我們的結果
f: 目標函數，也可以說是x和y之間的pattern，他定義了x和y之間實際上的關係，因為f是未知的，所以這也是後們想透過機器學習來學到的
D: 即資料，每一組資料包含了x和他相對應的y。d={(x1, y1)…..}
g: 我們希望透過機器學習學到f，但事實上我們並不一定真的能得學到f。所以我們希望機器學習可以學到一個假說(hypothesis)的函數g，而且和f越接近越好

上面可以看到機器學習的流程，透過資料餵給機器學習的演算法來學習到一個函式g，並且可以和f可以很像，這裡的f即是指資料的一種隱藏pattern，而且是未知的，而函式g會從hypothesis的集合內選出一個最符合資料的hypothesis。

機器學習常常被和很多不同領域搞混或是分不出清楚，在課程也有說明機器學習和不同領域的關係

Machine Learning vs Data Mining

資料探勘簡單來說是指，期望從資料庫中大量的資料出發，並從中找到一些有趣的發現來回答問題。以超市來說，會希望透過銷售的資料來找到一個人買了一樣商品後，是否也會買另一樣商品(像是之前的尿布與啤酒都市傳說)。但如果在資料探勘中想要找到有趣的事情，是指要找到一個假說G來作預測的話，那這裡的資料探勘就等同於機器學習。但資料探勘並非都會專注在作預測，有時可能只是想找到一些關聯性。

所以機器學習和資料探勘兩個領或可以說是密不可分的，甚至兩者是可以互補的。比如說可以透過資料探勘找到有趣的性質可以幫助機器學習找到好的假說(可以用在摘取好的特徵值)，或是透過機器學習的假說來幫助資料探勘找到有趣的發現。

Machine Learning vs AI

人工智慧: 希望電腦能夠作出智慧的表現，來完成一件事情(開車、下棋、預測)

有很多的方法可以達到不同的人工智慧任務，以下棋來說，傳統的人工智慧作法會設計演算法，透過分析一個game tree(下某一步棋的好處和壞處)來讓電腦自動下棋。如果是使用機器學習方法的話，就是設計演算法來可以告訴機器怎麼下棋會贏怎麼下會輸，然後讓機器分析後自己決定怎麼下(Alpha GO)。所以可以說，機器學習是實現人工智慧的一種方法。

Machine Learning vs Statistics

統計:使用資料來推論原本不知道的事情(ex: 丟銅板的機器)

機器學習中的假說G實際上是一個推論的結果，F則是一個我們不知道的事情，所以統計可以說是實現機器學習的一種方法。我們可以透過很多傳統統計的工具來實現機器學習，將這些工具借過來，使用機器學習的角度來看他。

參考資料:
Machine Learning Foundation 01

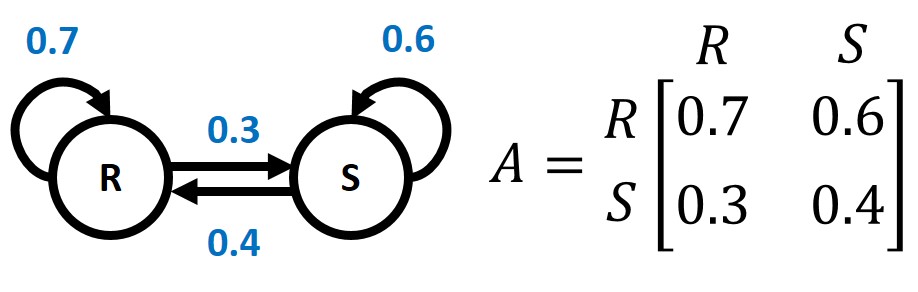
隱馬可夫模型(Hidden Markov Model, HMM)是一種具有隱含未知參數的馬可夫鏈(Markov Chain)，隱馬可夫模型常被使用在許多AI與Machine Learning的應用。既然隱馬可夫模型是一種馬可夫鏈，一開始先來簡單介紹一下什麼是馬可夫鏈

馬可夫鏈是指從一個狀態轉移到另一個狀態的隨機過程，且下一個狀態只能由當前狀態決定，根據機率分布從一個狀態轉移到另一個狀態，或是保持目前狀態，不同狀態間改變的機率稱為轉移機率(Transition Probability)。

以上面的例子來說明，這是一個具有兩個狀態的馬可夫鏈，S1是雨天(Rainy)，S2是晴天(Sunny)。其中S1可以轉移到S2也可以保持在S1，S2可以轉移到S1，也可以保持在S2。使用天氣變化這個例子來說明的話，可以表示成如果今天是雨天，明天可能是晴天也可能維持雨天。

如果我們有一個地區的天氣變化歷史紀錄，就可以統計出此地區晴天和雨天的轉移機率，並算出未來是晴天或是雨天的機率。假設已經知道今天是雨天，我們就可以從上面的樹狀範例可以輕易的計算出後天是雨天的機率是0.61，也可以使用矩算運算來算出後天是雨天和晴天的機率。

再來開始談談什麼是隱馬可夫模型，在隱馬可夫模型被隱藏起來不可見的就是狀態本身，雖然狀態被隱藏起來看不到了，但是卻可以透過「觀察序列」來間接的透露出狀態的訊息。

以wiki上面的天氣例子來說明，假設我本來每天都可以直接看到我居住地區的天氣狀態，有一天我搬家了沒辦法直接觀察原本地區的天氣狀態。雖然我無法直接看到原本地區的天氣狀態，但是我知道住在原本那個地區的朋友，在雨天的時候會有10%機率出門散布、40%機率出門購物，和50%在家打掃；在雨天的時候會有60%機率出門散布、30%機率出門購物，和10%在家打掃。

隱馬可夫模型讓我們可以透過觀察「看得到的」現象去推測另一個「看不到的」現象。以上面舉的例子來說，雖然我無法得知該地區的天氣狀況，但是我就可以透過觀察朋友每天的連續行為，來推測該地區的天氣狀況，並且以上面的方式來呈現一個隱馬可夫模型。

通常隱馬可夫模型有三大重要的問題:

1. 已知HMM模型，找出一個特定輸出序列的機率
2. 已知HMM模型，找出一個特定輸出序列的隱藏狀態序列
3. 未知HMM模型，找到最可能的狀態轉移和輸出機率

不同的演算法都有相對應的演算法可以使用，後續有機會再陸續介紹

參考資料:
Wiki - Hidden_Markov_model
演算法筆記 - HiddenMarkovModel
隱馬可夫模型：探索看不到的世界的數學工具
馬可夫鏈

Python中的decorator是一種對python語法的轉換寫法，使用decorator可以更方便的對函式作修改，也可以提高程式的可讀性。但是decorator只是一種語法糖，使用decorator並不會對語法產生改變，只是讓程式寫法可以更加的簡潔，並且讓開發者可以更方便的使用。

下面開始來說明一下，如何使用decorator來實作在函式的修改:

假設我們寫了一個執行sql的函式:

1
2

def select_execute(sql):    
    return 'execute select sql query!'

如果我們想要對這個執行sql的函式，用一個debug模式來包起來，並在debug模式印出執行的sql與執行的時間，這時可以透過closure來處理函式

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

def debug_query(func):    
    def debug_execute(sql):        
        exec_msg = func(sql)        
        exec_time = datetime.now()        
        debug_msg = """        
        Execute: {sql}        
        Result: {exec_msg}        
        Execute Time: {exec_time}"""        
        return debug_msg.format(**locals())    
    return debug_execute
    
>>> sql = 'SELECT * FROM TABLE'
>>> select_execute(sql)  # 不使用debug模式來執行select sql
execute select sql query!

>>> func = debug_query(select_execute)  # 使用debug模式來執行select sql
>>> func(sql)
Execute: SELECT * FROM TABLE
Result: execute select sql query!
Execute Time: 2017-05-20 16:09:08.953792

從上面的範例可以看到，先將執行sql的函式傳入外部函式，並在內部函式捕捉後，加上debug要印的部份進行改寫，這樣就可以將執行sql的函式包裝成debug模式。下面是使用decorator的寫法

1
2
3
4
5
6
7
8

@debug_query
def select_execute(sql):    
    return 'execute select sql query!'

>>> select_execute(sql)
Execute: SELECT * FROM TABLE
Result: execute select sql query!
Execute Time: 2017-05-20 16:09:08.953792

只要透過@和改寫的函式名稱，就可以簡化函式傳遞的語法，讓程式碼可以更加簡潔並達到相同效果

decorator也可以支援帶參數，如果今天要簡單的多印出一行debug宣告，並指定是哪一種query type作說明，可以透過多加上一層outter函式來傳入參數

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

def debug_describe(query_type):    
    def debug_query(func):        
        def debug_execute(sql):            
            exec_msg = func(sql)            
            exec_time = datetime.now()            
            descirbe = 'It is {} debug mode'.format(query_type)            
            debug_msg = """            
            {descirbe}            
            Execute: {sql}            
            Result: {exec_msg}            
            Execute Time: {exec_time}"""            
            return debug_msg.format(**locals())       
        return debug_execute    
    return debug_query
    
>>> func = debug_describe('select')(select_execute)  # 不使用decorator寫法
>>> func(sql)
It is select debug mode
Execute: SELECT * FROM TABLEResult: execute select sql query!
Execute Time: 2017-05-20 16:09:08.962798

@debug_describe('select')
def select_execute(sql):    
    return 'execute select sql query!'
    
>>> select_execute(sql)  # 使用decorator寫法It is select debug mode
Execute: SELECT * FROM TABLE
Result: execute select sql query!
Execute Time: 2017-05-20 16:09:08.962798

參考資料:
PythonDecorators
Understanding Decorators in Python
Python Decorator 四種寫法範例 Code

generator本身也是iterator，和iterator不同的地方在於generator會透過function宣告的方式，但有別於一般的function直接return回傳值，generator的function會在”有需要”的時候，使用yield來回傳值。為什麼稱為”有需要”的時候呢？因為generator在每次呼叫next()回傳值後，會記下所有的資料並保留最後一次執行狀態，直到下一次呼叫next()才會再繼續執行未結束的狀態。我們可以看一下下面這個範例:

1
2
3

def transform(data):    
    for char in data:        
        yield chr(ord(char) + 1)  # 透過yield回傳值後留存狀態

在每一次呼叫next()時，generator才會開始執行，並且每次執行到yield回傳值後停止，並保留執行狀態直到下一次呼叫next()才繼續執行。當generator終止後呼叫next()則會發生StopIteration。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

>>> char = transform('python')
>>> next(char)
q
>>> next(char)
z
>>> next(char)
i
>>> next(char)
p
>>> next(char)
p
>>> next(char)
o
>>> next(char)
Traceback (most recent call last):
File <stdin>, line 1, in     
    next(char)StopIteration

也可以使用for loop來呼叫generator

1
2
3
4
5
6
7
8
9

for char in transform('python'):     
    print(char)

q
z
u
i
p
o

使用generator最大的好處在於可以有效的處理一次性使用大量使用Memory的情況，將要一次性處理的過程拆成generator分次執行。例如當需要讀取很大的檔案處理時(甚至是多個很大的檔案)。而且使用generator可以降低iterator在loop的維度，讓程式碼可以更加的乾淨。

1
2
3
4
5
6
7
8
9

def get_line_title(file_name):    
    for file in file_name:        
        for line in open(file, mode='r', encoding='utf-8'):            
            if line.istitle():                
                yield line

>>> lines = get_line_title(file_name)
>>> for line in lines:
>>>     print(line)

上面的範例會產生generator並逐次判斷每一行內容，並回傳所有的標題。其中會用到兩個for loop和一個邏輯判斷，我們可以改寫成下面這樣，把讀取的部份和邏輯判斷的部份拆開來。

1
2
3
4
5
6
7
8
9
10

def get_line(files):    
    for file in files:        
        for line in open(file, mode='r', encoding='utf-8'):            yield line
        
def get_title(lines):    
    return (line for line in lines if line.istitle())
    
>>> all_line = get_line(file_name)
>>> for title in get_title(all_line):
>>>     print(title)

如果善用generator可以有效的管理Memory的使用，也可以讓程式碼更加的有可讀性!

參考資料:
Python Docs - Generators
Iterators & Generators
Introduction to Python Generators

python中有些資料結構是可以透過for來loop裡面所有的item的，像是list, tuple, dict, str還有file都可以。在使用上其實for迴圈會呼叫物件中的iter()，此函式會回傳一個Iterator(迭代器)，Iterator會透過next函式來一次一次的取得下一個item，並在沒有下一個item的時候拋出StopIteration來告訴for迴圈迭代結束。

像這種有按照Iteration Protocol定義iter和next的物件又被稱為Iterable

1
2
3
4
5

>>> for item in [1, 2, 3, 4]
>>> for item in (1, 2, 3, 4)
>>> for item in {'one': 1, 'two': 2}
>>> for item in 'python'
>>> for line in open('file')

如果希望自己定義的物件是Iterable，只要透過在class內實作iter和next(讓python的build-in函式iter()和next()可以呼叫)就可以達成。

假設我們建立了一個物件可以設定一個字串，並在每次iteration的時候透過ascii回傳每個字元的下一個字元

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

class Transform:    
    def init(self, data):        
        self.data = data        
        self.i = 0        
        self.n = len(data)    
    
    def iter(self):        
        return self    
        
    def next(self):        
        if self.i == self.n:            
            raise StopIteration        
        item = chr(ord(self.data[self.i]) + 1)        
        self.i = self.i + 1        
        return item

宣告一個Transform物件，並用for來讀取每一個值

1
2
3
4
5
6
7
8
9

>>> t = Transform('python')
>>> for item in t:  # for迴圈自動叫iter()，並用next()來作iteration
>>>     print(item)
q
z
u
i
p
o

宣告一個Transform物件，並呼叫iter並用next來讀取每一個值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

>>> t = Transform('python')
>>> t2 = iter(t)
>>> next(t2)
q
>>> next(t2)
z
>>> next(t2)
u
>>> next(t2)
i
>>> next(t2)
p
>>> next(t2)
o
>>> next(t2)  # 當沒有下一個item之前，會產生StopIteration
Traceback (most recent call last):
File <stdin>, line 1, in     
    next(t2)
StopIteration

除了透過定義iter和next讓自己的物件為iterable，也可以透過在class中定義getitem來達成。兩者只要有定義其中一種，都可以讓for loop來依序讀取物件中的item

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

class Transform:    
    def init(self, data):        
        self.data = data        
        self.i = 0        
        self.n = len(data)    
        
    def getitem(self, i):        
        return chr(ord(self.data[i]) + 1)
        
>>> t = Transform('python')
>>> for item in t:  # 透過定義__getitem__也可以讓物件為iterable，並可以使用在for loop
>>>     print(item)
q
z
u
i
p
o

參考資料:
Python docs - Iterators
Python docs - Iterator types
Python docs - Iterable