第二講的內容主要在說明如何透過機器學習來回答兩元問題。上一講有提到機器學習會透過一個演算法A,並透過資料D和假說Hyposis H集合,透過選擇一個假說來學習到函式g。以上一講的案例來說,我們會透過函式g來決定要不要發信用卡。

我們可以簡單的透過計算分數的方式來建立一個簡單的機器學習方法。首先可以把每位使用者的資料建立一筆特徵向量當作輸入資料,而每個維度還會有重要性的權重(例如年薪的權重可能會比性別的權重還來的高),最後把每個使用者依據加總的分數,和設定的門檻值(threshold)比較,如果高過門檻值就發卡,沒高過就不發卡,這樣的模型h就是一個簡單的Perceptron(感知器)。
其實在情感分析(Sentiment Analysis)上,以前也常用這種計算分數的方式來判斷文本屬於正面(Postive)或是(Nagtive)。當我們手上有一個情感詞典(定義哪些字是正面,哪些字是負面),在拿到一篇文章的時候,就可以加總正面詞(+1)和負面詞(-1)來算出文章的情感分數,再搭配門檻值來判斷文章是屬於正面還是負面,甚至是正負面的程度。(不同字詞可以有不同程度的權重,沒有被情感詞典定義的詞當作0分)
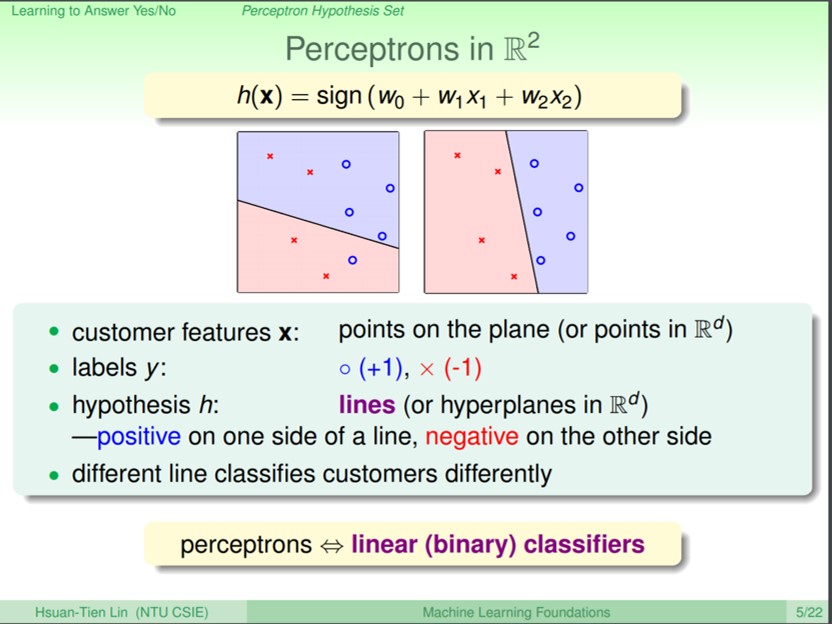
這個用來判斷要不要發信用卡的模型h,在二維的平面上會呈現為一條直線(平面上的每一點就是一筆資料x,每一筆資料的形狀則是指的label),在高維度的空間會是一個平面。這條直接的一邊是其中一種label(O),跨過線的另一邊則是另一種label(X),這樣的線性分類器即可以用來分類兩元問題。

那究竟平面上面的這條線該怎麼切才是最好的呢?可以透過Perceptron Learning Algorithm(PLA)來學習出最好的線性分類器。當平面上的線如果切的不夠好時,透過會旋轉這條線來讓切線更完美。當正的label被分到負的label時,代表w和x的角度太大,可以透過向量相加來讓角度變小;當負的label被分到正的label時,代表w和x的角度太小,可以透過向量相減來讓角度變大。就這樣一直轉到所有的正的label和負的label都分到正確的類別沒有任何分錯,就可以得到一個最佳的切線,這個演算法稱為PLA。
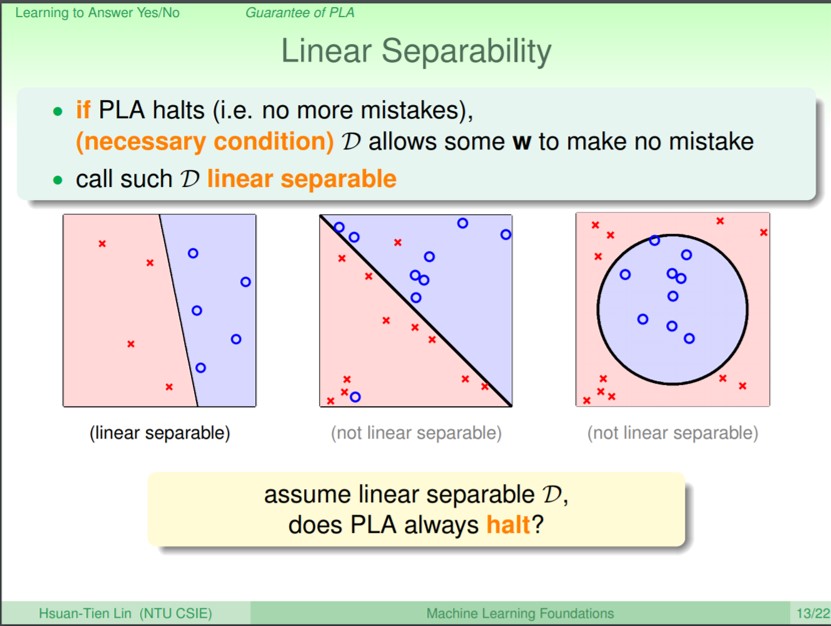
PLA既然要在平面上找到一條切線,那勢必他就必須要是線性可分的問題,像是上圖最左邊就是一個線性可分的問題,右邊兩張則是線性不可分,即不管怎麼旋轉這條切線都沒辦法把兩種類別各自分到對的地方。如果稍有瞭解支援向量機(Support Vector Machine, SVM)的人大概會想到,如果使用SVM的話就可以解決線性不可分的問題,因為SVM主要是也在空間裡找到線性可分的超平面來切分空間,如果遇到第二種線性不可分的情況,最簡單可以透過調整懲罰參數C來忽略一些無法分到正確類別的資料(也許是雜訊)。至於遇到第三種情況的話,則可以調整核函式Kernel Function來將於N維線性不可分的資料於較高的維度M找到線性可分的超平面。

回到PLA,現實上絕對沒有這麼好的情況可以讓你都有線性可分,也許只有稍微有點雜訊,就會讓問題變成線性不可分。這邊會用到演算法稱為口袋演算法(pocket algorithm),即是在PLA的修正學習過程中,如果找到一個比較好的線(即分錯最少),我們就把這條線放到口袋裡面,當遇到下一條比我們口袋裡這條線更好的線,就再換成新的線,一直到執到覺得應該差不多就停下來。所以當我們是線性可分,PLA可以幫助找到好的解答;但如果不是線性可分,透過變形的PLA確實可以找到一個還不錯的解答。